Math background
Contents
Sets
Set a collection of distinct elements:
- \({a, b, c, d}\) - finite
- \(\mathbb{R}\) : real numbers - infinite
- \({x \in \mathbb{R}: cos(x) > 1/2}\) - set with restriction
Notations:
- \(\Omega\) - universal set(set that contain all objects)
-
\(\in\) - is member of
- \(2 \in \{1, 2, 3, 4\}\)
-
\(\notin\) - is not member of
- \(2 \notin \{1, 3, 5\}\)
-
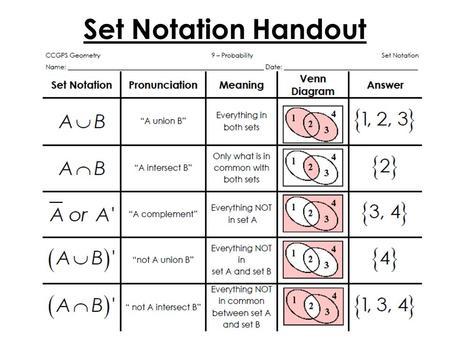
\(A’\), \(A^c\), \(\overline{\rm A}\) - \(A\) compliment, everything not in \(A\)
- \(x \in S^c if x \in \Omega, x \notin S\)
-
\(\emptyset\) and \(\varnothing\) or \(\{ \}\) - empty set
- \(\Omega^c = \emptyset\)
-
\(\cup\) - union, everything in both sets
- \(\{1, 2, 3\} \cup \{3, 4, 5\} = \{1, 2, 3, 4, 5\}\)
- \(x \in S \cup T \leftrightarrow x \in S \, \textsf{or} \> x \in T\)
- \(\cup_{n} S_{n}\) - union of all \(n\) sets
-
\(\cap\) - intersection, only what is in common in both sets
- \(\{1, 2, 3\} \cap \{2, 3, 4\} = \{2, 3\}\)
- \(x \in S \cap T \leftrightarrow x \in S \, \textsf{and} \, x \in T\)
- \(\cap_{n} S_{n}\) - intersection of all \(n\) sets
-
\(\subset\) - subset of set
- \(\{1, 2, 3\} \subset \{1, 2, 3, 4, 8\}\)
-
\(\supset\) - superset of set
- \(\{1, 2, 3, 4, 8\} \supset \{1, 2, 3\}\)
Sets properties
- \(S \cup T = T \cup S\)
- \(S \cap (T \cup U) = (S \cap T) \cup (S \cap U)\)
- \((S^c)^c = S\)
- \(S \cup \Omega = \Omega\)
- \(S \cap S^c = \emptyset\)
- \(S \cap \Omega = S\)
- \(S \cup (T \cup U) = (S \cup T) \cup U\)
- \(S \cup (T \cap U) = (S \cup T) \cap (S \cup U)\)
De Morgan’s laws
- \((S \cap T)^c = S^c \cup T^c\)
- \((\cap_{n} S_{n}^c) = \cup_{n} S_{n}^c\)
- \((S \cup T)^c = S^c \cap T^c\)
- \((\cup_n S_{n}^c) = \cap_n S_{n}^c\)
Countable versus uncountable infinite sets
Countable: can be put in 1-1 correspondence with positive integers:
- Positive integers
- Integers: \(0, 1, -1, 2, -2, …\)
- Pairs of positive integers
- Rational numbers \(q\), with \(0 < q < 1\), \(1/2, 1/3, 2/3, 1/4, 2/4, …\)
Uncountable: not countable:
- The interval [0, 1]
- The reals
- The plane
Sequences and their limits
Sequence is some collection of an elements:
- \(a_1, a_2, a_3, …\)
- sequence \(a_1\)
- \(\{a_i\}\)
- formal - function \(f: \mathbb{N} -> S, f(i) = a_i\)
When does a sequence converge:
- If \(a_i \leq a_{i + 1}\) for all \(i\), then either:
- the sequence “converges to \(\infty\)”
- the sequence converges to some real number \(a\)
- if \(|a_i - a| \leq b_i\) for all \(i\), and \(b_i -> 0\), then \(a_i -> a\)
Series
Infinite series
\(\sum_{i=1}^{\infty} a_i = \lim_{n -> \infty} \sum_{i=1}^n a_i\) (provided limit exists)
- if \(a_i \geq 0\): limit exists
- if terms \(a_i\) do not all have the same sign:
- limit need not exist
- limit may exist but be different if we sum in different order
- Fact: limit exists and independent of order of summation if \(\sum_{i=1}^{\infty} |a_i| < \infty\)
Order of summation in series
only if \(\sum |a_{ij}| < \infty\), then:
- \(\sum_{i \geq 1, j \geq 1} a_{ij} = \sum_{i=1}^{\infty}(\sum_{j = 1}^{\infty} a_{ij}) = \sum_{j=1}^{\infty}(\sum_{i = 1}^{\infty} a_{ij})\)
- \(\sum_{(i, j) : j \leq i} a_{ij} = \sum_{i=1}^{\infty} \sum_{j=1}^{i} a_{ij} = \sum_{j=1}^{\infty} \sum_{i=j}^{\infty} a_{ij}\)
Arithmetic progression
\begin{equation*}
a_{n}=a_{1}+(n-1)d
\end{equation*}
\begin{equation*}
a_{n}=a_{m}+(n-m)d
\end{equation*}
\begin{equation*}
S_n = \frac{n}{2}[2a_1 + (n - 1)d]
\end{equation*}
\begin{equation*}
S_n = \frac{n}{2}[a_1 + a_n]
\end{equation*}
\begin{equation*}
\overline{\rm n} = S_n / n
\end{equation*}
\begin{equation*}
\overline{\rm n} = \frac{a_1 + a_n}{2}
\end{equation*}
where:
- \(a_1\) is the first term of an arithmetic progression.
- \(a_n\) is the nth term of an arithmetic progression.
- \(d\) is the difference between terms of the arithmetic progression.
- \(n\) is the number of terms in the arithmetic progression.
- \(S_n\) is the sum of n terms in the arithmetic progression.
- \(\overline{\rm n}\) is the mean value of arithmetic series.
Geometric progression
\begin{equation*}
a_n = ar^{n - 1}
\end{equation*}
\begin{equation*}
a_n = ra_{n - 1}
\end{equation*}
\begin{equation*}
S_n = \frac{a_1 (1 - r^n)}{1 - r}
\end{equation*}
\begin{equation*}
S_n = \frac{a_1 - a_n * r}{1 - r}
\end{equation*}
\begin{equation*}
where r \ne 1
\end{equation*}
where:
- \(a\) - initial value
- \(r\) - common ratio
Simplified: \(S = \sum_{i=0}^{\inf} \alpha^i = 1 + \alpha + \alpha^2 + … = \frac{1}{1 - \alpha}\), if \(|\alpha| < 1\)
pass
Other
If \(X\) is a vector, and \(X \in \{-1, 1\}^{n}\), then \(X^{T}X == n\), where \(n\) is a constant, and \(n == len(X)\).