Probability Models and Axioms

Contents

Sample space
- Sample space: discrete/finite example
- Sample space: continuous example
Probability axioms
Probability calculations
Countable additivity
- Countable additivity axiom

Sample space

Describe possible outcomes
Describe beliefs about likelihood outcomes

Possible outcomes:

List (set) of possible outcomes, $\Omega$ (omega)
List must be:
- Mutually exclusive
- Collectively exhaustive
- All the “right” granularity

Interpretation and uses of probabilities:

Measure frequency of the event
Description of beliefs / betting performance

Sample space: discrete/finite example

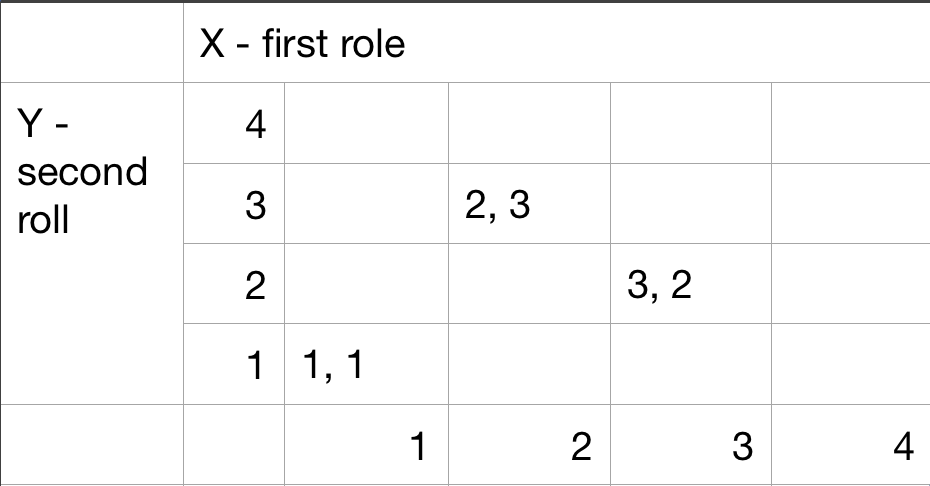
$/images/math/probability-theory/probability-models-and-axioms/01_discrete_example.png$

Table description

Sequential description

Two rolls of a tetrahedral die.

Sample space: continuous example

$(x, y)$ such that $0 \leqslant x, y \leqslant 1$

$/images/math/probability-theory/probability-models-and-axioms/03_continuous_example.png$

Probability axioms

Event: is a subset of the sample space. Probability is assigned to events

$/images/math/probability-theory/probability-models-and-axioms/event.png$

Axioms:

Nonnegativity: $P(A) \geqslant 0$
Normalization: $P(\Omega) = 1$
(Finite) Additivity: if $A \cap B = \varnothing$, then $P(A \cup B) = P(A) + P(B)$

Some simple consequences of the axioms:

$P(\varnothing) = 0$
$P(A) + P(A^c) = 1$
if $A_1, …, A_k$ disjoint, then $P(A \cup … \cup A_k) = \sum_{i=1}^{k}P(A_i)$
$P(\{S_1, S_2, …, S_k\}) = P(\{S_1\} \cup \{S_2\} \cup … \cup \{S_k\}) = P(\{S_1\}) + … P(\{S_k\}) = P(S_1) + … + P(S_k)$

More consequences of the axioms:

if $A \subset B$, then $P(A) \leqslant P(B)$ (img 1)
$P(A \cup B) = P(A) + P(B) - P(A \cap B) = P(A) + P(A^c \cap B)$ (img 2)
$P(A \cup B) \leqslant P(A) + P(B)$ - union bound
$P(A \cup B \cup C) = P(A) + P(A^c \cap B) + P(A^c \cap B^c \cap C)$ (img 3)

$/images/math/probability-theory/probability-models-and-axioms/conseq_of_axioms.png$

Probability calculations

Discrete finite example

Discrete uniform law:

Assume $\Omega$ finite consist of $n$ equally likely elements
Assume $A$ consist of $k$ elements, then

$P(A) = k * frac{1}{n}$

every outcome prob == $\frac{1}{16}$

$P(X = 1) = 4 * \frac{1}{16}$
let $Z = min(X, Y)$
- $P(Z = 4) = 1/16$
- $P(Z = 2) = 5 * \frac{1}{16}$

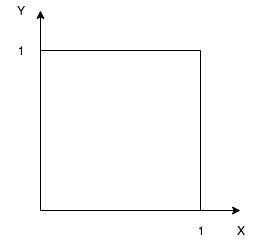
Discrete continuous example

Suppose we have $(x, y)$ such that $0 \leq x, y, \leq 1$

Uniform probability law: Probability = Area

$P(\{(x, y) | x + y \leq 1/2 \})$ = triangle area = $\frac{1}{2} * \frac{1}{2} * \frac{1}{2}$

$P(\{0.5, 0.3 \})$ = area of one point = $0$

Probability calculations step

Specify sample space
Specify a probability law
Identify an event of interest(if possible - graphical way)
Calculate …

Countable additivity

Let’s we have sample space $\{1, 2, 3, … \}$

$P(n) = \frac{1}{2^n}, n=1, 2..$

$\sum_{n=1}^{\infty} \frac{1}{2^n} = \frac{1}{2} \sum_{n=0}^{\infty} \frac{1}{2^n} = \frac{1}{2} * \frac{1}{1 - 1/2} = 1$

P(outcome is even) = $P(\{2, 4, 6, … \} ) = P(\{2\} \cup \{4\} \cup ..) = P(2) + P(4) + .. =$

$= \frac{1}{2^2} + \frac{1}{2^4} + … = \frac{1}{4}(1 + \frac{1}{4} + \frac{1}{4^2} + …) = \frac{1}{4} * \frac{1}{1 - 1/4} = \frac{1}{3}$

Countable additivity axiom

Strengthens the finite additivity axiom:

if $A_1, A_2. A_3$ is an finite sequence of disjoint events, then $P(A_1 \cup A_2 \cup A_3 …) = P(A_1) + P(A_2) + P(A_3)$
additivity holds only for “countable” sequence of events
the unit square(similarly the real line, etc.) is not countable. (It’s elements cannot be arranged in a sequence)
“Area” is a legitimate probability law on the unit square, as long as we do not try to assign probabilities/areas to “very strange” sets